今回は材料力学の基礎をおさらいしていきます。分量が多いので数回に分けていきます。教科書を読んで理解するとともに、演習で実力を身に付けていくことが重要です。レベルとしては機械設計技術者試験2級、技術士1次試験を想定しています。
重要な公式集まとめ
フックの法則
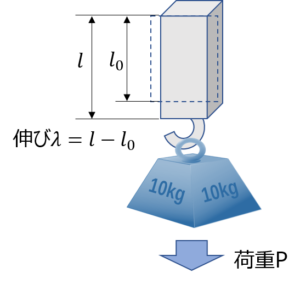
\(\sigma =\dfrac{P}{S}\)
応力=荷重÷断面積
\(\varepsilon =\dfrac{\lambda }{l}\)
ひずみ=伸び÷初期長さ
\(\sigma =E\times \varepsilon \)
応力=ヤング率×ひずみ
ポアソン比
丸棒を引っ張ると伸びるが、同時に棒の直径は縮みます。また、丸棒を圧縮すれば棒の直径は増えます。この比率をポアソン比といいます。

\(\nu=\left| \dfrac{\varepsilon `}{\varepsilon }\right| \)
\(\varepsilon =\dfrac{l-l_{0}}{l_{0}}=\dfrac{\lambda }{l_{0}}\)
\(\varepsilon ‘=\dfrac{d-d_{0}}{d_{0}}=-\dfrac{\lambda ‘}{l_{0}}\)
演習1 丸棒の変形と伸びの関係
(問)密度ρ、重力加速度gとして、直径d、ヤング率E、ポアソン比\(\nu\)の丸棒の軸方向に引張荷重Pを加えた場合、丸棒の直径はいくつになるか。
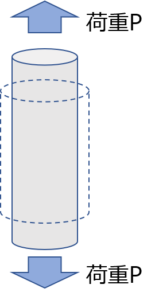
(解答)丸棒の初期直径と変形後の差を\(\Delta d\)とすると\(\Delta d=\nu \varepsilon _{x}d\)
フックの法則から\(\varepsilon _{x}=\dfrac{\sigma _{x}}{E}=\dfrac{ P| S}{E}=\dfrac{P}{E\dfrac{\pi d^{2}}{4}}=\dfrac{4P}{E\pi d^{2}}\)
よって丸棒の直径は\(d-\Delta d=d-\nu \varepsilon _{x}d=d-\nu\times \dfrac{4P}{E\pi d^{2}}\times d=\left( 1-\dfrac{4P\nu }{E\pi d^{2}}\right) d\)となる。
演習2 自重を考慮したときの棒の最小断面積
(問)一様な断面積をもつ長さ\(l\)の棒の長さの下端に引張荷重Pが作用する。棒の許容応力を\(σ\)とすると、棒の自重を考慮して破断しない最小断面積はいくつか。

(解答)棒の付け根が最も応力が大きくなり、荷重Pと棒の自重をすべて受ける。
棒の許容応力\(\sigma >\left( P+\rho glS\right) /S\)
よって、断面積\(S >\dfrac{P}{\sigma -\rho gl}\)となる。
演習3 円管と丸棒の構造物の変形量
(問)長さ\(l\)の丸棒を円管Bに入れ上下から剛体で挟み圧縮する。圧縮荷重がPのときの構造物の変形量(縮み量)はいくつか。丸棒の断面積を\(S_{A}\)、円管の断面積を\(S_{B}\)、丸棒のヤング率を\(E_{A}\)、円管のヤング率を\(E_{B}\)とする。
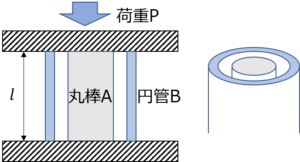
(解答)圧縮荷重Pは丸棒Aにかかる荷重\(P_{A}\)と円管Bにかかる荷重\(S_{B}\)に分けられる。
丸棒Aの変形量と円管Bの変形量は等しく\(\Delta l\)とする。
丸棒Aの変形量は
\(\Delta l=l\varepsilon _{A}=l\dfrac{\sigma _{A}}{E_{A}}=l\dfrac{P_{A}/S_{A}}{E_{A}}=\dfrac{P_{A}l}{E_{A}S_{A}}\)
同様に円管Bの変形量は
\(\Delta l=l\varepsilon _{B}=l\dfrac{\sigma _{B}}{E_{B}}=l\dfrac{P_{B}/S_{B}}{E_{B}}=\dfrac{P_{B}l}{E_{B}S_{B}}\)
丸棒Aにかかる荷重は
\(P_{A}=\dfrac{\Delta l E_{A}S_{A}}{l}\)
円管Bにかかる荷重は
\(P_{B}=\dfrac{\Delta l E_{B}S_{B}}{l}\)
これにより\(P=P_{A}+P_{B}=\dfrac{\Delta l \left( E_{A}S_{A}+E_{B}S_{B}\right) }{l}\)
よって、\(\Delta l =\dfrac{Pl}{E_{A}S_{A}+E_{B}S_{B}}\)となる。
まとめ
ヤング率(縦弾性係数)とポアソン比は意味合いをしっかりと理解して瞬時に答えられるようにおきましょう。
直感的に硬い材質ほどヤング率が大きいほど硬く、ヤング率が小さいほど柔らかい材質ということがわかると思いますが、ポアソン比は単位はなく、物体に荷重をかけると生じる縦と横方向のひずみのことです。
ちなみにひずみは漢字で「歪み」ですが、ゆがみと混同するのでひらがなで表記します。
例えば、ひずみゲージで計測を行うというようなときに使います。
詳しくはこちらの共和電業のひずみゲージのページが参考になると思います。




コメント