今回は材料力学の基礎②として、はりの曲げをおさらいしていきます。材料力学の4番バッター、はりの曲げを攻略しましょう。レベルとしては機械設計技術者試験2級、技術士1次試験を想定しています。
重要な公式集まとめ
たわみ
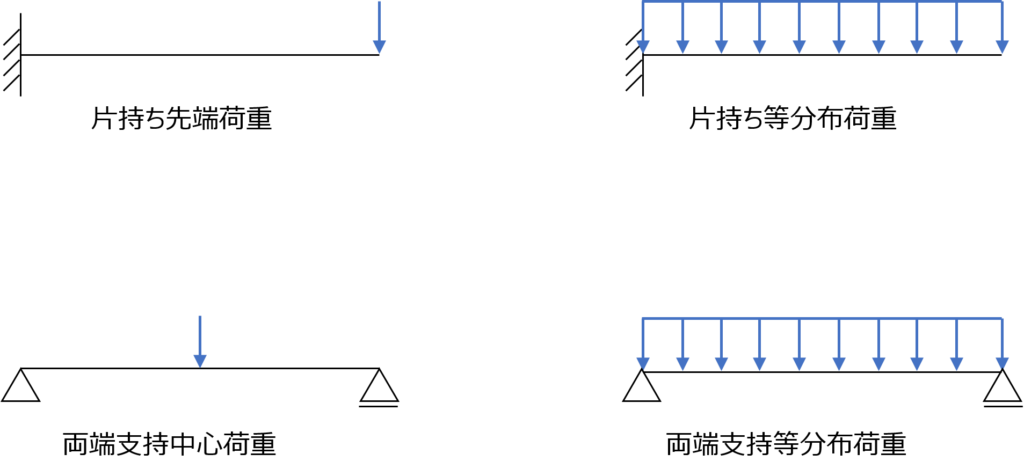
片持ち先端荷重\(\delta =\dfrac{Pl^{3}}{3EI}\)
片持ち等分布荷重\(\delta =\dfrac{wl^{4}}{8EI}\)
両端支持中心荷重\(\delta =\dfrac{Pl^{3}}{48EI}\)
両端支持等分布荷重\(\delta =\dfrac{5wl^{4}}{384EI}\)
モーメント
\(M=Fl\)
モーメント=力×回転中心からの距離
演習1 集中荷重と等分布荷重の関係
(問)長さ\(l\)の片持ちばりに対し、左図のように先端に集中荷重Pを作用させる場合と、右図のように等分布荷重wを作用させるときの最大曲げ荷重が等しい。このときPとwの関係はどうなっているか。

(解答)左図の曲げモーメントは\(M_{a}=Pl\)
右図の等分布荷重は、はりの中心の位置に集中荷重\(wl\)が負荷されていることと置き換えられる。
これにより曲げモーメントは\(M_{b}=wl\times \dfrac{l}{2}=\dfrac{wl^{2}}{2}\)
題意より\(M_{a}=M_{b}\)であり、\(Pl=\dfrac{wl^{2}}{2}\)と表される。
よって\(P=\dfrac{wl}{2}\)となる。
演習2 単純支持 集中荷重のはりのたわみ
(問)長さ\(l\)の単純支持はりの中央に集中荷重Pが作用しているときの、はりのたわみを求めよ。はりの剛性はEIとする。
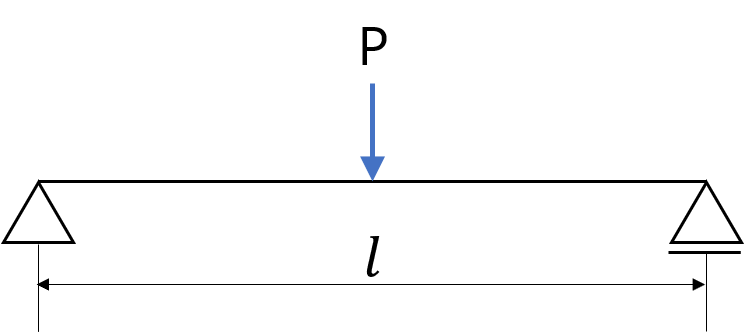
(解答)はりの中央で分割すると、片持ち先端荷重はりのたわみが左右に発生していることと等価になる。
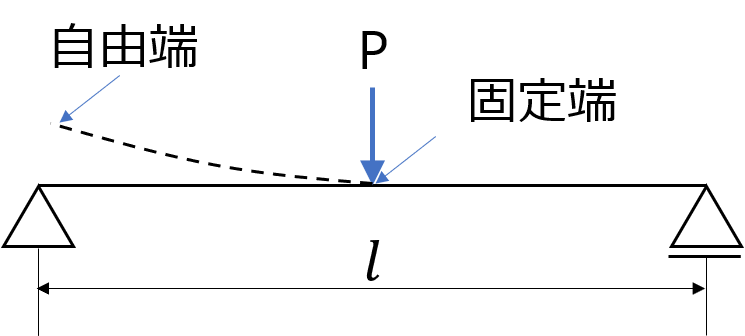
片持ち先端荷重のたわみの公式\(\delta =\dfrac{Pl^{3}}{3EI}\)となる。
ここで中心から支点までの距離\(l/2\)より
\(\delta =\dfrac{\left( \dfrac{P}{2}\right) \left( \dfrac{l}{2}\right) ^{3}}{3EI}=\dfrac{Pl^{3}}{48EI}\)となる。
演習3 単純支持 等分布荷重のはりのたわみ
(問)長さ\(l\)の単純支持はりに等分布荷重wが作用しているときの、はりの最大曲げモーメントを求めよ。
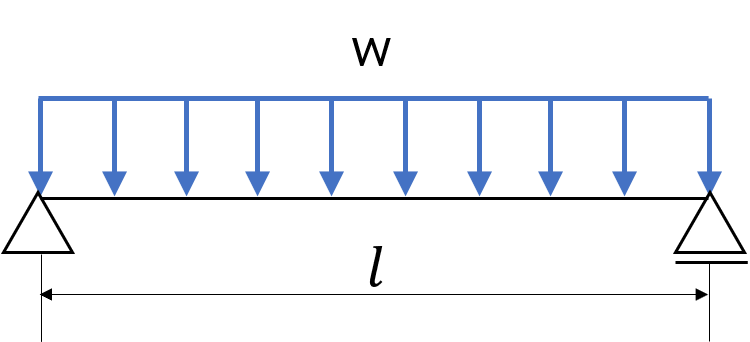
(解答)はりの両端の反力はそれぞれ\(wl/2\)となる。はりの中央で分割すると、はりの左端点に時計回りに\(wl/2\)が作用し、中央から\(l/4\)の位置に半時計回りに\(wl/2\)が作用する。
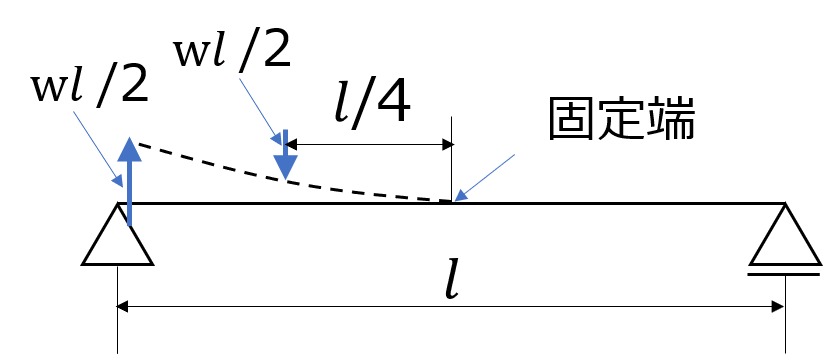
よって、はりの最大曲げモーメントは\(M=\dfrac{wl}{2}\cdot \dfrac{l}{2}-\dfrac{wl}{2}\cdot \dfrac{l}{4}=\dfrac{wl^{2}}{8}\)となる。
まとめ
はりの曲げに関する問題は頻出で、実務でもはりの強度計算は行うと思いますのでしっかり解けるようにしましょう。等分布荷重は集中荷重に置き換えられることと、片持ち、両端支持、両端固定のはりの変形モードは図としてイメージをしておくことで、モーメントのつり合いがスピーディーにできると思います。諦めずに何度でも復習してマスターしましょう。




コメント